Gravitation class 9 notes

NOTES PREPARED BY 

ASHAQ HUSSAIN BHAT 

GL TEACHER SCHOOL EDUCATION 

DEPARTMENT JAMMU AND KASHMIR

GRAVITATION

Introduction 

There is an interesting story that, Newton was sitting under an apple tree. Suddenly, an apple fell on him. He drew the conclusion that a net force should have acted on the apple to make it fall from the tree. This event made Newton imagine that perhaps all bodies in the universe are attracted towards each other in the same way as the apple was attracted towards the earth. This force of attraction is called gravitational force or force of gravitation. Now in this blog we will learn about gravitation in detail.

Gravitation

The force that causes acceleration and keeps the stone moving along the circular path is acting towards

the centre of the earth. This force is called centripetal force. The force which is needed to make an object travel in a circular path is called centripetal force. The centripetal force acting on the moon is provided by the force of attraction of the earth.

UNIVERSAL LAW OF GRAVITATION

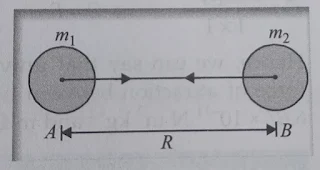
According to this law ,the force of attraction between two particles or bodies is directly proportional to the  product of their masses  and inversely proportional to the square of their distances  between these particles or bodies 

consider two bodies  A and B having mass m1 and m2 respectively  . let the distance between these bodies be R

According to the law of gravitation, the force of attraction (F) or force of gravitation between these bodies is given by ;       

 F∝ m1 m2........................................i

 and F ∝1/R2.....................................ii

Combining equations (i) and (ii), we get

and F ∝m1m2/R2

or F = G m1m2/R2...........................iii

where G is a constant and is known as "universal gravitational constant. 

Equation (iii) is the mathematical form of Newton's law of gravitation. Here the magnitude of the force

varies inversely with the square of the distance between the two particles. So this law is also called inverse square law

According to the inverse square law, force of gravitation F ∝ 1/R2

When the distance is R, then force, F ∝1/R2

When the distance is 2R (doubled), then F' ∝1/(2R)2

From these two relationships, one can write

F/F =1/(2R)2 XR2/1

= 1/4 or 

F = F/4

Thus, when the distance between the two particles is doubled, the gravitational force becomes

one-fourth.

When the distance is R/2 (halved), then F ∝ 1/(R/2)2

From these relationships, F/F= 1/(R/2)2 /1/R2

= R²X4/R² = 4 OR F = 4F

 

Thus, when the distance between the two particles is halved, the gravitational force becomes four times,

Unit and Value of Gravitational Constant

According to Newton's law of gravitation, force between two bodies of masses m1, and m2 separated by a distance R is given by

F = Gm1 m2/R2 ....................................i

Rearranging, we get Gm1m2 = F x R²

or  G= FXR2/m 1 m 2 ................................ii

The SI unit of G can be obtained by putting the units of force, distance and mass, thus SI unit of G is N m² kg

If m1 = m2 = 1 kg and R = 1 m, then from equation (ii)

⇒ G= F x (1)2/1x1

⇒ G=F

Hence, we can say that universal gravitational constant G is numerically equal to the gravitational

force of attraction between two bodies of unit masses placed at unit distance. The value of G in S I is

6.67 x 10-11N m² kg² and in CGS is 6.67 x 10 dyne cm² g ².

Importance of the Universal Law of Gravitation

The gravitational force is one of the fundamental forces in nature. The gravitational force is responsible for the existence of the solar system (motion of planets around the sun).

• the existence of life on the earth.
• rainfall and snowfall.
• holding the atmosphere near the surface of the earth.
• motion of the moon around the earth.
• occurrence of tides.
• predictions about solar and lunar eclipses made on the basis of this law always come out to be true.

Characteristics of Gravitational Force

(i) Gravitational force between two bodies or objects does not need any contact between them. It means, gravitational force acts at a distance.

(ii) Gravitational force between two bodies varies inversely proportional to the square of the distance between them. Hence, gravitational force is an inverse square force.   

(in) The gravitational force between two bodies or objects form an action-reaction pair. If object A attracts object B With a force F1 and the object B attracts object A  with a force F2 then  F₁ =-F₂

Estimation of Gravitational Force between Different Objects

The formula applied for calculating gravitational force between light objects and heavy objects is the same, F =Gm₂ m₂/R²

Let us take three different cases :

• Gravitational force between a body of 1 kg and the earth

Let a body of mass 1 kg be placed on the surface of the earth as  The distance between the centre of the earth and body is equal to the radius of the earth i.e., R = 6.4 x 10 m. The magnitude of gravitational force between the earth and the body is given by F=

i.e., F =Gm₂ m₂/R²

where, m₁ = 1 kg

m₂ = 6 x 10²4 kg (mass of the earth)

R = 6.4 x 106 m
G= 6.67 x 10-¹¹ N m² kg 2

 F = 6.67x10-¹¹1 N m² kg- 2 x1 kg ×6×10²4 kg  N/             =   9.8 N
                          (6.4 x 106 m)²

Thus, a body of mass 1 kg is attracted by the earth with a force of 9.8 N.

Gravitational force between the sun and the earth

Mass of the earth, m₁ = 6 x 10²4 kg
Mass of the sun, m₂ = 2 x 1030 kg
Distance between the sun and the earth, R = 1.5 x 10¹¹ m
Gravitational force between the sun and the earth,

F =Gm₂ m₂/R² =  6.67 x 10-11 N m² kg 2    x6x1024  X 2 X 1030kg/       =  3.6 × 1022 N 
                                          (1.5x 10¹¹ m)²

The gravitational force between the sun and the earth is very large (i.e., 3.6 × 1022 N). This force

keeps the earth bound to the sun.

Gravitational force between the moon and the earth

Mass of the earth, m1, = 6 x 1024 kg

Mass of the moon, m₂  = 7.4 x 1022 kg
Distance between the moon and the earth, R = 3.8 x 108 m
Gravitational force between the earth and the moon,

F= Gm₂ m₂ = 6.67 x 10-11 N m² kg 2   x6x1024 kgx7.4x10²²  kg = 2.05x1020N
          R²         (3.8 x 108 m)²

                

This large gravitational force keeps the moon moving around the earth.  We find that,

1. the gravitational force between two small bodies is very small.
2. the gravitational force between a small body and a larger body (e.g. the earth) is large.
3. the gravitational force between two large bodies (e.g., the sun and the earth) is very large.

Gravitational Force and Newton's Third Law of Motion

According to Newton's third law, to every action there is always an equal and opposite reaction. It means  if an object A exerts some force on another object B, then the object B exerts an equal and opposite force on the object A at the same instant. This law applies to the force of gravitation also.

fig

According to Newton's second law of motion, force = mass x acceleration

i.e., for a given force, acceleration produced varies inversely as the mass. 

We know that acceleration produced in a body of mass 1 kg due to gravitational pull of earth on it is

9.8 m s. As this acceleration is very large, we can see the body falling towards earth. We shall show that

when gravitational pull of same magnitude acts on earth (where mass is 6 x 10 kg), the acceleration

produced in earth is 1.63 x 1024 m s-2. As this value of acceleration is too small, we cannot see the earth

moving towards the falling body of mass 1 kg.

Centre of Mass and Centre of Gravity

The point in a body where its whole mass is assumed to be concentrated is called its centre of mass. The centre of mass of a homogeneous sphere or cube must lie at its geometric centre. A rigid extended body is a continuous distribution of mass. Each particle or portion of the body experiences the force of gravity. The net effect of all these forces is equivalent to the effect of a single force, mg acting through a point called centre of gravity of the body, or we can say that a point in any body at which the force of gravity on the whole of the body can be assumed to act is called its centre of gravity. On the surface of the earth, or near it, where the force of gravity is constant, the centre of mass also becomes the centre of gravity. If we assume the earth to be a sphere of uniform density, then its centre of mass lies at its centre. The force of attraction of the earth on any body is, therefore, towards its centre.

Application of Newton's Law of Gravitation

Determination of the masses of planets and stars

Knowing precise values of g, R and G, it is possible to determine accurately the mass of any planet or

star by using the relationship, M= gR2      [R is radius of planet or star and g is value of acceleration due to gravity on the star or planet]

                                                     G

Estimating the masses of double stars 

A double star is a system consisting of two stars orbiting around their common centre of mass. The

extent of irregularity in the motion of a star due to the gravitational pull by the other star bound to it,

can be used for estimating their masses. This a small irregularity in the motion of a star is called wobble. Many double stars outside our solar system have been detected in recent years by measuring the irregularity (called wobble) in the motion of stars.

Free Fall

The motion of a body towards the earth when no other force except the force of gravity acts on it is
called a free fall. Thus all the freely falling bodies, lighter or heavier, fall towards the earth with the
same acceleration.

According to Galileo Galilei, if there were no air, all the bodies having different masses when dropped
simultaneously from the same height would hit the ground at the same time.

Later Robert Boyle proved this experimentally. He placed a coin and a feather in a long glass tube
and removed its air with the help of vacuum pump. When the tube was inverted both the coin and
the feather fell to the bottom of the tube at the same time. Thus the acceleration produced in all freely
falling bodies is same and does not depend upon the mass of the falling body.

Acceleration due to Gravity of the Earth

The acceleration produced in a body due to the gravitational pull of the earth near its surface is called
acceleration due to gravity of the earth. The gravitational force acting on a body of mass m near the
surface of the earth is given by,

 F= G. m x M/R2..................................i

where, m is the mass of the body, M is the mass of earth, and R is the radius of the earth.
If g is the acceleration produced in a body of mass m, then

F=mxg.......................................................ii

...From eq (i) and (ii)

mg  = G m x m/R2

or g = GM/R2 .........................................iii

From equation (iii), we see that acceleration produced in the body due to the earth does not depend upon its mass.

Gravity and Gravitation

The terms gravity and gravitation are not same. The force of attraction between any two objects by

virtue of their masses is called gravitation (or gravitational force), For example, force of attraction between any two objects such as books, tables, chairs, and between any two heavenly bodies are the examples of gravitation. The force of gravitation exerted by a huge heavenly body such as, the earth, the moon, or the sun etc., on a smaller object near its surface is called its gravity (or force of gravity). for example, earth pulls an object of mass 1 kg towards it with a force of 9.8 N. So, force of 9.8 N is the gravity (force of gravity) of the earth. Similarly, on the surface of moon, we can talk about the gravity of the moon. Thus, we see that the gravity is a particular case of gravitation.

Mass and Weight

Mass

The quantity of matter in a body is called its mass. Mass is a measure of the number of atoms contained in any body. Since the number of atoms in any object remains constant, hence its mass remains constant. Mass is expressed in mass units. The SI unit of mass is kilogram (kg).

Mass is usually denoted by m.

The characteristics of mass of a body are as follows:

• Mass is a scalar quantity.
• Mass of a body does not depend on the shape, size and the state of the body.
• Mass of a body is proportional to the quantity of matter contained in it.
• Mass of a body can be measured with the help of a common balance.

Weight

The force with which a body is attracted by the earth is known as the weight of the body. It varies from place to place. The weight of a body on earth is equal to the force of gravity exerted by the earth on that body. We have, F = ma (From Newton's second law)

W = mg..........................................i

where g is the acceleration due to gravity. The S.I. unit of weight is same as that of the force, i.e., newton (N). From equation (i) it is clear that weight of a body depends upon the mass of the body and value of acceleration due to gravity g at a place. The characteristics of weight of the body are as follows:

• Weight is a vector quantity.
• Weight is measured with a spring balance, or by a weighing machine.
• The weight of a body is directly proportional to its mass.
• The weight of a body changes with the value of g. So when g decreases, the weight of the body also decreases..
• The value of g at the poles is higher than that at the equator, so the weight of a body is greater on the poles than that on the equator. weight of a body is different on different planets.
• The value of g on the surfaces of different planets of the solar system are different, therefore, the The value of g decreases with height from the surface of the earth. Therefore, the weight of the body also decreases with height from the surface of the earth. That is why, the weight of a man is less on the peak of Mount Everest than the weight of the man at Delhi.
• The value of g decreases with depth from the surface of the earth. Therefore, the weight of a body decreases with depth from the surface of the earth.
• The value of g at the centre of the earth is zero, hence weight of the body is also zero at the centre of the earth.

Weight of an Object on the Surface of Moon

Consider an object of mass m on the surface of the earth. Let M be the mass of the earth and R be its radius. According to universal law of gravitation, the force with which the earth attracts the object is given by  F=GMm/R² ...........................i

 
Since, force with which the earth attracts the object = weight of the object (W) i.e., F=W
.: Equation (i) becomes,
W =GMm/R².........................................ii

Now, let this object of mass m lies on the surface of the moon. Let M be the mass of the moon and R

be the radius of the moon. Therefore, according to universal law of gravitation, the force with which the

moon attracts the object is given by

F' =GMm
        R²m

But F' = weight of the object on the moon (Wm)

:. Wm =GMmm/....................................iii
              R²m

Dividing equation (iii) by equation (ii), we get

Wm    =     GMmm  x      R2      =   MmR2
W                R2m              GMm        MR2m

Now, M(mass of earth) - 5.98 x 1024 kg
Mm (mass of moon) = 7.36 x 10²3 kg
R(radius of earth) = 6400 km = 6.4 x 106 m
Rm, (radius of moon) = 1740 km = 1.74 x 106 m
Put these values in equation (iv), we get

Wm=        7.36x1022 x (6.4×106)²  =       1   = 0.166
 W               5.98 x 10²4 x (1.74×106)²    6

Wm =     1    W
               6

Thus, weight of an object on the surface of moon =1/6 x Weight of the object on the surface of the earth.

For this reason, moon exerts less force of attraction on objects.

Kepler's Laws of Planetary Motion

Johannes Kepler gave the following three laws to explain the motion of the planets. These laws are called Kepler's laws.

(i) Law of orbits

Each planet moves around the sun in an elliptical orbit with the sun at one of the foci of the orbit as shown in figure.

 This law is called Kepler's first law of planetary motion.

(ii) Law of areas

The line joining the sun and planet sweeps out equal areas in equal intervals of time. This law is called as shown in fig below 

Kepler's second law. It means areal velocity (-area traced/ time) of the planet around the sun is constant

. In the figure shown the sun is at O which is one of the foci of the elliptical orbit. If the time of travel of the planet from P₁ to P₂ is the same as that from P3 to P₁, then according to this law,

Area of OP₁P₂ = Area of OP3P4

Since, arc P₁ P₂ is smaller than the arc P, P₁. It means that the speed of the planet is greater when it is closer to the sun, than its speed when it is farther away from the sun. Thus, according to Kepler's second

law, a planet does not move around the sun with a constant speed.

(iii) Law of periods

The square of the time taken by a planet to complete a revolution around the sun is directly proportional to the cube of semi-major axis of the elliptical orbit. This law is called Kepler's third law of planetary Motion

i.e., T2  ∝  r3 or T 2 = constant   x  r3

i.e.  T2 /  r3     =   Constant

Derivation of Newton's Inverse Square Rule from Kepler's Third Law

Newton derived mathematically his universal law of gravitation from Kepler's third law of planetary motion

Consider a planet of mass m revolving around the sun of mass M in a circular path of radius r. Let us take as the orbital velocity of the planet and T as its time period to complete one revolution around the sun. The distance travelled by the planet in one complete rotation is = 2𝛑r.

We have, velocity, v=Distance travelled/Time taken

i.e.,V=  2𝛑r.

               T

or

V∝ r/T          (2𝛑 Is constant)

Squaring both sides of equation (ii), we get

v² = r2/T2 or   v² ∝ r2/T2 x r/r.............................iii

According to Kepler's third law of planetary motion,r3/T2 is constant 

.. From equation (iii)

v²  ∝1/r.................................................................iv

Now we know that the centripetal force  F required to keep the planet in circular orbit is

F = mv2/r

F ∝ v² /r  .......................................................... v       (m is constant  )  

From equation (iv) and (v), we get

F ∝ 1/r2

This is Newton's inverse square rule.