motin class 9

 NOTES PREPARED BY 

ASHAQ HUSSAIN BHAT

TEACHER SCHOOL

 EDUCATION DEPARTMENT 

JAMMU AND KASHMIR

Introduction of Motion

Motion means change in position of an object with respect to its surroundings in a given interval of time. We see various things around us in motion, e.g. water flowing in a river, flowers nodding to blowing wind, birds flying in the sky, a player running in the playground and many more. Motion is a relative phenomenon, i.e., an object appearing to be in motion to one person can appear to be at rest to another person, e.g. to a person driving a car, trees on roadside might appear to move backward while same tree will appear to be at rest to a person standing on roadside.

Describing Motion

Two different physical quantities the distance and the displacement, are used to describe the overall motion of an object and to locate its final position with reference to its initial position at a given time. Since motion is a relative concept, we need a reference point to describe the position of an object. We call this reference point as origin.

Consider an object moving in a straight line. Let the object starts from a point O. This starting point o is taken as the reference point. After 10 minutes, it reaches the position P3 through P, and P2

(time taken from O to reach P3= 10 min)

(time taken to move from P3to P2 - 5 min)

In next 5 minutes, it comes back to position P2 (40 m away from O) and stops. So the total distance travelled by the object in these 15 minutes is

OP3 + P3P2 = 60 + 20 - 80 m.

But the shortest distance between the initial and final positions of the object - OP, = 40 m. The shortest length of the path between initial and final positions is known as displacement.

So, in the above example, 

Distance covered by the object - 80 m

Displacement of the object - 40 m right from O.

 Thus distance is described with magnitude only whereas displacement requires both the magnitude and

the direction. Physical quantities like distance, which can be described by magnitude only are called scalars, and the quantities which are described using both magnitude and direction are called vectors. Hence distance is a scalar quantity and displacement is a vector quantity.

Difference between distance and displacement :

(1) Distance in always positive but displacement may be zero, negative or positive.

(ii) Displacement can not exceed distance. The maximum value of displacement in distance which occurs when a body moves on a straight line in one direction. 

(iii) Distance is a scalar quantity but displacement is a vector quantity. Therefore displacement has both magnitude as well as direction. 

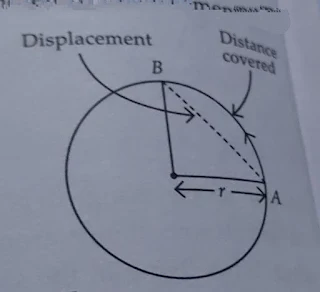
(iv) When a body moves on a curved line, we measure displacement covered by measuring the least distance between initial and final points.

Following example illustrates it.

If a particle moves on a circular path with radius r. It starts from point A and reaches point B.

Distance covered = length of curved line AB =πr/2

The displacement between points A and B = length of straight line AB = √2r.

(v) When a body returns back to the originating point, displacement becomes zero but distance covered is positive

Similarities between distance and displacement :

(1) Both distance and displacement have same unit of measurement, in S.I unit it is metre.

(ii) Both distance and displacement have magnitude. If the body travels on a straight line unidirectionally, both becomes equal in magnitude. 

Uniform and Non-uniform Motion

Uniform Motion:-

An object is said to be in uniform motion if it covers equal distances in equal intervals of time, howsoever big or small these time intervals may be.

For example, suppose a car covers 60 km in first hour, another 60 km in second hour, again 60 km in the third hour and so on. The motion of the car is uniform. Let us now understand the meaning of the words, (howsoever small the time interval may be) used in the definition. In this example, the car travels a distance of 60 km in each hour. In the stricter sense, the car should travel 30 km in each half hour; 15 km in every 15 minutes; 10 km is every 10 minutes, 5 km is every 5 minutes and 1 km in every one minute.

Only then, the motion of the car can be said to be uniform. However, in broader sense, we do not mind it when time interval is big. The motion of the car is taken as uniform when it covers a distance of 60 km in every one hour.

Non-uniform Motion

Consider a bus starting from one stop. It proceeds slowly when it passes crowded area of the road. Suppose it manages to travel merely 100 m in 5 minutes due to heavy traffic. When it gets out and the road is clear, it speeds up and is able to travel about 2 km in 5 minutes. We say the motion of bus is non-uniform. i.e. it travels unequal distances in equal intervals of time. Example of non-uniform motion is, a speeding up or a slowing down vehicle.

Speed and Velocity

Speed:-

Speed of a moving body gives us the idea about how fast or slow the body moves. In case of  vehicles, it is the quantity indicated by their speedometers. 

Mathematically, it is the distance travelled by the object in unit time. We usually denote it by symbol v.

v = Distance travelled in unit time.

Its SI unit is metre per second represented by the symbol m/s or m sl. It is a scalar quantity as it requires magnitude only for its specification.

When a body moves with non-uniform speed, the magnitude of its speed changes. The value of speed at a particular movement is called instantaneous  speed. 

A body starting from rest will have instantaneous speed equal to zero, when t = 0. Its instantaneous speed will go on increasing every moment when the motion is under acceleration. While mentioning instantaneous speed, we must mention the particular time or moment. The speedometer of a vehicle gives the value of

instantaneous speed.

Velocity (Speed with Direction)

The distance covered by a body per unit time in a specified direction is called the velocity. Thus, the quantity that specifies both the speed and direction of an object is called velocity. It is denoted by symbol v. S.I. unit of velocity is m/s. Larger unit such as km/h is also used.

Uniform Velocity : If the velocity of an object does not change as time passes, it is said to move with a uniform velocity. In such a case, both its speed and direction remain constant. This means that the object is moving along a straight line, without turning back, with a fixed speed. The displacement of the particle is equal in equal time intervals, howsoever small a time interval we choose. We also say in this situation that the object is in uniform motion.

Non-Uniform Velocity : If the velocity of a moving body does not remain constant in a given interval of time, we say the body has a non-uniform velocity in that time interval. A body is said to have non-uniform velocity if

(i) its speed, i.e. magnitude of velocity changes and direction remains constant.

(ii) its direction of motion changes and speed remains constant, e.g., a boy running on a circular track with a constant speed of 2 m/s.

(iii) both speed and direction change.

Speed and velocity share similar relation as distance and displacement do.

Thus, speed=distance travelled/time taken

and velocity=displacement/time taken

There are many instances when displacement of an object is zero while distance travelled is non-zero. Thus, velocity of an object can be zero or have some other non-zero value (depending on displacement) different from its speed.

Relative velocity: The concept of relative velocity is very helpful in studying the motion of two objects with respect to each other. The following example will clarify it. Suppose distance between A and B is 1 km, and both move in a single direction with A moving at 5 m/s and B moving at 4 m/s. We have to find out how much time A will take to catch B.

Here A is moving towards B (going closer to B) at the rate of 5-4=1 m/s

Distance of separation is 1 km = 1000 m.

So this separation will be covered up in time =1000

Thus, 5-4=1 m/s is called the relative velocity of A with respect to B.

Suppose A and B are moving in opposite direction (towards each other). In that case relative velocity is equal

is 5+ 4 = 9 m/sec and time taken for A to catch up with B =1000/5+4= 1000/9=111.11 s

Acceleration

In non-uniform motion, velocity varies with time. The rate at which velocity varies is called acceleration. We can say that acceleration is the change in velocity per unit time. 

If the velocity of an object varies from an initial value "u" to the final value "v" in time "t", then acceleration "a" is given by  a = v-u/t

This is also called average acceleration. As noted, velocity is a vector quantity, so is the acceleration. The SI unit of acceleration is m s-²'or m/s-²

Analysis of the equation, a =v-u/t

Study of Motion Through Various Graphs

If information about various quantities related to motion is given in tabular form for various instants of time it can be converted in graphical form. It makes easier for us to find out relation between various physical quantities

. 

Distance-Time Graph

(i) Distance is taken along y-axis and time is along the x-axis. A convenient scale is chosen for both the axes. Consider the following data taken by an observer for a bus in 5 s. Using this data, we can obtain the distance - time graph for the bus as shown:

Distance (m)             Time (s)

0                                      0

2                                      1

4                                       2

6                                       3

8                                       4

10                                     5

  

We see, the graph is a straight line passing through the origin (intersection of two axes). It is clear that the bus is travelling 2 m in each second, or the body has a constant speed. Let us find out speed of the bus from above graph. By definition, speed of a body is given by 

v=total distance travelled/total time taken

distance-time graph gives the speed of the object.

(ii) If distance-time graph of an object is a straight line parallel to the time axis, as shown in graph, we say the position of the object does not change with time, or the object remains at rest. Here slope of line is Zero hence velocity is zero,

(iii) If we get a curved line in distance-time graph, if we find that slope for any two time intervals, will not be same. Or we say the object has a non-uniform speed, i.e. the body is accelerated. Slope at point P is more than that at point Q. Hence velocity increases with time.

Displacement-Time Graph

We know that displacement of an object can be negative also, while distance is always positive. Thus, displacement-time graph differs from distance-time graph in the following manner: First, when the object moves with a uniform velocity, it is given by

the slope of line OA. Velocity =AP/OP

After that, object moves with a constant velocity which is given by the slope of line AB.

Now, slope of line AB =SB-SA/tB-tA

                          = 0-6/6-3

                          = -6/3

                            =  -2

It is negative.

We say, the object moves with velocity -2 m/s. i.e. with a velocity 2 m/s in opposite direction. It comes to original position in 6 sec (net Time (s)displacement zero) and then moves to the other side maintaining its velocity

Velocity-Time Graph

In this graph, variation of velocity of an object with time is shown. Time is taken along x-axis while velocity is taken along y-axis.

• For uniformly accelerated motion 

Consider the velocity-time graph shown. It is a straight line with a positive slope passing through the origin. Consider any two positions A and B of the object, at instants tī and t2 when the object has velocities u and v respectively.

Now according to definition of acceleration,

a=∆v/∆t=v-u/t²-t¹        eq (1st) 

=AC/BC= slope of the straight line

Thus, slope of the graph obtained in a velocity time graph gives the acceleration of the object. Now for a straight line, the slope will be same for any two points considered. Or we can say that acceleration will remain constant or uniform.

Thus, a uniformly accelerated motion is shown by a straight line having a positive slope in a

time graph.

Consider equation (i),

a=v-u/t²-t¹

Let t² - t¹=t

=> a=v-u/t

v=u + at

which is one of the very important equations of motion.

For a uniform motion : When an object is in uniform motion, it will have a constant velocity at every instant. i.e. velocity won't change with time or we can say that velocity-time graph is a straight line parallel to time-axis.

Now acceleration between any two instants t1, and t2 is

a=Δυ/∆t=v-v/t²-t¹= 0

Velocity (m/s)

Thus, acceleration is zero for an object having uniform motion. Also according to the definition of velocity,

 total displacement

Average velocity=total displacement/total time taken

Again taking same time interval between two instants t¹and to t²

v=S/t²-t¹

=s=v x (t2 - +t¹) = AB× BC

= Area of the shaded region shown in adjacent graph.

Thus distances of the object is given by the area enclosed by velocity-time graph and the time axis. Distance can also be obtained for a uniformly accelerated motion using the same method. 

For example: Total distance = area of trapezium ABEDA

s = Area of rectangle BCDE + Area of triangle ABC.

= BE× ED +{½×AC×BC =u× (t² – t¹)+(½v–u)×(t²– t)

Let time interval t²-t¹=t

s=ut +½(v-u) t

Using equation, v=u + at, we get

 => S=ut +½(at)t

S=ut +½at²

This is second equation of motion.

Consider the figure given above once again,

s = Area of trapezium ABEDA =½×ED(BE + AD) 

=½t(u + v) ½(v-u/a (v+u) 

= ½a(v²-u²) or

=>V²-u²=2aS

• For uniformly retarded motion : 

For this, velocity-time graph is a straight line having a negative slope. 

• For non-uniformly accelerated motion :

 For this, velocity-time graph can have any shape depending upon how the velocity varies. Here, acceleration will be different between different instants as the slope does not remain constant. The graphs discussed above can also be used to make a comparative study of motion of two or more objects. Consider the illustration given. 

Uniform Circular Motion

If an object moves in a circular path with uniform speed, its motion is called uniform circular motion.

A circular path can be made up of an indefinite number of small sides, and a body moving along such a circular path changes its direction of motion continuously. Therefore, if you run on a circular track, you change your direction infinite times in one round. Four arbitrary points on the circular path and the direction of motion of the body at these points are shown. Since the direction of motion changes, uniform circular motion is a case of accelerated motion. Direction of acceleration is always towards centre and its magnitude is v2/r at all points

Note: If a body moves on a circular path of radius r and completes one rotation in time t, then the distance

covered by the body is equal to the circumference of the circle, i.e., 2 πr. In such a case speed v is given by, v=2πr/t

Examples of circular motion

• A stone tied to a thread and whirled in a circular path. 
• Wheels of various vehicles rotating about their axles.
• A satellite revolving around the Earth in a circular path at constant speed.
• The Moon revolving around the Earth in a circular path at constant speed.

In the above examples, the speed is uniform but the velocity is variable due to continuous change in direction. Thus, the bodies have an accelerated motion.....